A theoretical physicist at RIKEN has developed an expression for the maximum speed at which changes in macroscopic systems can occur. This will improve our understanding of quantum phenomena in non-equilibrium systems.
The Heisenberg uncertainty principle, which states that it is impossible to simultaneously determine an object’s position and momentum, is one of the most difficult aspects of quantum mechanics to grasp. In other words, the greater the precision with which a particle’s position is determined, the greater the range of its possible momentum (and vice versa).
In 1945, two physicists, Leonid Mandelstam and Igor Tamm, focused on another type of uncertainty relation, one between time and energy fluctuation, and demonstrated that transitions in quantum systems do not occur instantaneously; rather, the speed at which a transition occurs is capped by an amount determined by how much the system’s energy fluctuates.
Many other so-called quantum speed limits have since been derived, aiding in the understanding of quantum physics and being useful in a variety of quantum applications.
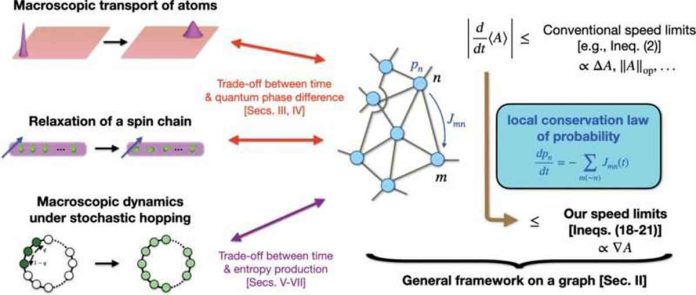
However, significant issues arise when quantum speed limits are applied to macroscopic systems. “Previous quantum speed limits, which are useful for small systems, typically become meaningless for macroscopic transitions,” says RyusukeHamazaki of the RIKEN Hakubi Research Team’s Nonequilibrium Quantum Statistical Mechanics. “Conventional quantum speed limits, for example, give an infinite upper bound for the speed of transitions in an atomized gas.”
Hamazaki has now deduced a quantum speed limit for transitions in macroscopic systems.
He says, “This new derivation provides fundamental limits that can be applied to various types of non-equilibrium quantum macroscopic phenomena.” “I hope that the concepts introduced in this study will lead to the emergence of many fundamental laws and applications concerning macroscopic quantum dynamics.”
Hamazaki arrived at the stricter quantum speed limit by developing a general framework based on the probability conservation law, a fundamental principle in physics.
The discovery of a new trade-off relationship was an unexpected outcome for Hamazaki. “Instead of the Mandelstam-Tamm bound’s trade-off relationship between time and energy fluctuation, I discovered one between time and the gradient of the quantum phase—a fundamental quantity in quantum physics.”
Hamazaki plans to expand his strategy to see if it can be used to derive quantum speed limits for quantities such as quantum entanglement growth.

”…of many fundamental laws and applications concerning macroscopic quantum dynamics.”
(-RyusukeHamazaki-)
Does the “Speed if Light” remain constant within the Quantum World?