Operations research at the MIT Sloan School of Management and the Institute for Data, Systems, and Society professor David Gamarnik have focused his attention on less-studied category of problems as they are more relevant to the everyday world. They involve randomness and it is an integral feature of natural systems. Gamarnik have developed a potent tool for analyzing these problems named overlap gap property. Gamarnik have described the new methodology in the Proceedings of the National Academy of Sciences.
Some computational problems in math and computer science are hard to solve. There is an entire class of problems which are impossible to solve algorithmically. There are also slightly “easier” problems that are less well-understood.
P ≠ NP
The most famous problem in theoretical computer science is “P ≠ NP”. This asks if problems involving vast datasets exist for which an answer can be verified relatively quickly. But whose solution, even if worked out on the fastest available computers, would take an absurdly long time.
P ≠ NP conjecture is unproven. But computer scientists believe that many familiar problems like the traveling salesman problem, fall into this impossibly hard category. The challenge is the salesman have to find the shortest route through N different cities. The question is simple when N=4 as there are only six possible routes to consider. But there are more than 1030 possible routes, for 30 cities. The numbers also rise dramatically from there. The problem comes in designing an algorithm that quickly solves the problem in all cases. Computer scientists believe that no such algorithm exists based on algorithmic complexity theory, so, P ≠ NP.
There are many other intractable problems like this. For example, you have a giant table of numbers with thousands of rows and columns. You have to find the precise arrangement of 10 rows and 10 columns such that its 100 entries will have the highest sum attainable, among all possible combinations.
Scientists are sure that there can’t be a fast algorithm that can efficiently solve problems like the saga of the traveling salesman.
Peaks and valleys
To understand the OGP, you need to understand how the idea arose. Physicists have been studying spin glasses, since 1970’s. This is a material with properties of both liquids and solids that have unusual magnetic behaviours. Spin glasses have provided a general theory of complex systems that’s relevant to problems in physics, math, computer science and materials science.
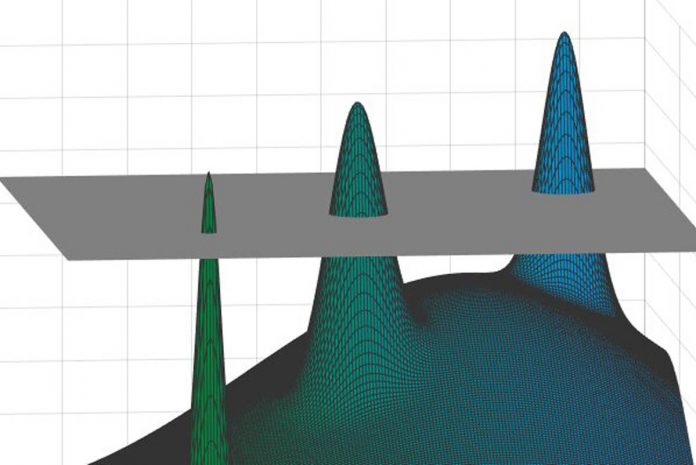
Physicists have faced difficulty while trying to predict the energy states. Particularly the lowest energy configurations of different spin glass structures. This situation is like a “landscape” of countless mountain peaks separated by valleys. The goal is to identify the highest peak. Here, the highest peak represents the lowest energy state.
Physicists think the picture can be simplified by slicing the mountains at a certain elevation and ignoring everything below that cutoff level. There will be a collection of peaks protruding above a uniform layer of clouds. Each point on those peaks representing a potential solution to the original problem.
Gamarnik have noticed something that had been previously overlooked. He saw the diameter of each peak will be much smaller than the distances between different peaks. If someone pick any two points on this sprawling landscape, they would either be very close or very far. There would be a telltale “gap” in these distances. Gamarnik have characterized this by the OGP.
Unlocking the secrets of algorithmic complexity
OGP can help scientists to assess the difficulty of creating fast algorithms to tackle particular problems. But this finding leaves scientists far away from being able to prove the nonexistence of fast algorithms that could solve these optimization problems in random settings. This proof could have provided a definitive answer to the P ≠ NP problem.