In a groundbreaking study, researchers have delved into the intricate world of complex systems, unraveling the mysteries behind their seemingly chaotic behaviors.
Published in Nature Physics, the study led by Vincent Thibeault from Université Laval in Québec, Canada, sheds light on the pervasive low-rank hypothesis that offers a key to understanding and modeling these complex structures.
Decoding the Complexity
Complex systems, from neural networks to ecosystems, exhibit nonlinear dynamics, posing challenges in predicting their behaviors.
These intricate structures involve numerous components with nonlinear interactions, making it difficult to foresee their actions based on individual parts.
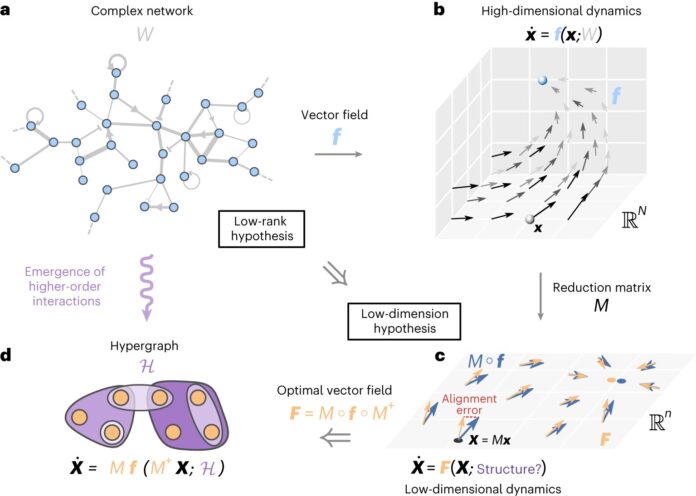
Thibeault and his team embarked on a journey to demystify these systems and find a path to effective dimension reduction for a clearer comprehension.
The Low-Rank Hypothesis Unveiled
The heart of the study lies in the low-rank hypothesis applied to high-dimensional nonlinear dynamical systems. Thibeault explains, “Despite the high dimensionality, the interactions within the intricate network exhibit low effective dimensions.”
This implies that by carefully selecting a few variables, the emergent macroscopic properties of complex systems can be adequately described.
However, caution is urged in choosing dimensions to avoid losing crucial system properties and creating unintended interactions.
Navigating the Complexity of the Brain
The researchers used the brain as a prime example of a complex system. Neurons, the fundamental elements, communicate through electrical signals.
When synchronized, this communication enhances information processing, but it can also lead to emergent phenomena like epilepsy.
Thibeault emphasizes the need for a balance in choosing dimensions, stating, “Care must be taken to avoid losing the salient properties of the system and even creating new types of interactions.”
Putting the Hypothesis to the Test
To validate the low-rank hypothesis, the team employed singular value decomposition (SVD), a powerful mathematical tool from linear algebra.
SVD dissects matrices into essential components, allowing researchers to scrutinize the underlying order in complex systems.
The goal was to find an optimal dimension for dimensionality reduction and determine if the dynamics of high-dimensional systems indeed hinge on the behavior of low-rank matrices.
Unraveling Patterns with SVD
SVD emerged as the key to unlocking the secrets of complex systems. Thibeault and his team meticulously applied this mathematical technique to analyze the dynamics of various networks.
The results showcased rapidly decreasing singular values, supporting the feasibility of effective dimension reduction.
This breakthrough opens avenues for a more streamlined understanding and modeling of complex system behaviors across disciplines.
A Paradigm Shift in Complexity
Thibeault’s study marks a paradigm shift in approaching the complexities of interconnected structures.
By embracing the low-rank hypothesis and leveraging SVD, researchers are poised to navigate the intricate world of complex systems with newfound clarity.
This breakthrough not only impacts physics, biology, sociology, and network science but also paves the way for advancements in predicting and harnessing emergent phenomena in diverse fields.
FAQ
The low-rank hypothesis in complex systems suggests that despite high-dimensional nonlinear dynamics, interactions within intricate networks exhibit low effective dimensions.
This implies that a careful selection of variables can sufficiently describe the emergent macroscopic properties of these systems.
Complex systems, such as neural networks and ecosystems, present challenges due to their nonlinear dynamics. Understanding these systems contributes to advancements in physics, biology, sociology, and network science, offering insights into emergent phenomena and self-organization.
The study was led by Vincent Thibeault, a Ph.D. student at Université Laval in Québec, Canada. His research, published in Nature Physics, explores the intrinsic simplicity of complex systems and the feasibility of effective dimension reduction.
SVD is a mathematical tool from linear algebra that dissects matrices into essential components. In the study, researchers, including Thibeault, used SVD to test the low-rank hypothesis, analyzing the dynamics of various networks and showcasing rapidly decreasing singular values.
The study used the brain as an example of a complex system. Neurons, the fundamental elements of the brain, communicate through electrical signals. The researchers explored how synchronization of neuron firing, despite the high dimensionality, exhibits low effective dimensions, impacting information processing and leading to emergent phenomena like epilepsy.
Researchers, including Thibeault, emphasized the need for caution when selecting dimensions to describe complex systems. Choosing dimensions requires a balance to avoid losing crucial system properties and inadvertently creating new types of interactions.
The study contributes by unveiling the underlying simplicity in complex systems through the low-rank hypothesis and SVD. This breakthrough allows for effective dimension reduction, offering a clearer understanding and modeling of complex system behaviors, with implications for diverse scientific disciplines.
The findings open avenues for advancements in predicting and harnessing emergent phenomena in complex systems. The streamlined understanding achieved through effective dimension reduction has potential applications in fields ranging from neuroscience to ecological studies.
More information: Vincent Thibeault et al, The low-rank hypothesis of complex systems, Nature Physics (2024). DOI: 10.1038/s41567-023-02303-0